CUANTILES
Los cuantiles se dividen en Cuartiles, deciles y percentiles.
CUARTILES
Estos representan el valor que está al 25%, 50% y 75% de la totalidad de los datos, estos se dividen en cuatro como su nombre lo indica.


DECILES
Del primero al noveno marcan el valor ubicado del 10% al 90% de los datos y su fórmula es:
PERCENTILES
Indican el valor que esta del 1% al 98%,99% de los datos y su fórmula es:
NOTA: para indicar que cuartil, decil, o percentil se está buscando se coloca con numero y se multiplica por n (numero de datos)
Ejemplo:
Pedro en una fiesta con sus amigos realizo una encuesta sobre las edades de sus amigos y las personas presentes y estos fueron los datos que obtuvo:
3, 5, 6, 25, 27, 27, 28, 28, 45, 47, 48, 48, 11, 14, 18, 18, 20, 24, 31, 33, 34, 36, 44, 50, 50, 52.
Con esto él quiere obtener el valor del 3 cuartil, 4 decil y 17 percentil:
Identificamos que el número de datos es 26
3 5 6 11 14 18 18 20 24 25 27 27 28 28 3 33 34 36 44 45 47 48 48 50 50 52
17 percentil= 14 4 decil= 27 3 cuartil= 45
MEDIA GEOMÉTRICA
Es una medida que se puede aplicar al crecimiento exponencial, ya que obtiene la raíz enésima de un grupo de n datos multiplicados entre sí, su fórmula es:
Ejemplo:
Alonso va a una tienda de sabritas y observa que los precios son los siguientes con los cuales desea obtener la media geométrica:

MEDIA ARMONICA
Se denota con la letra H, es una serie de n números es la reciproca a la media aritmética o media y su fórmula es:
ejemplo:
pilar tiene tres hermanos los cuales tienen las siguientes edades

Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización.
Son aquellas que nos señalan, el punto medio y que se agrupan alrededor del mismo, en ellas se encuentran: la media, mediana, moda, los perciles, y percentiles.
PARA DATOS NO AGRUPADOS

MEDIA
Para datos no agrupados se define como la suma de todos los datos divididos entre el número de los datos que se tengan, su fórmula es:
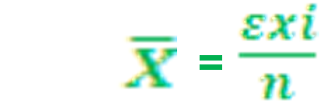
Por ejemplo
Tenemos los siguientes datos de edades de la casa de Lupe: 3, 9, 4, 8,5, 3. Se realiza lo siguientE:
MEDIANA
Es el valor central de los datos que pueden ser representados de manera par e impar, se encuentran en el centro de distribución de forma ordenada ascendente y descendente, si el número de datos es par la mediana es igual al promedio de los datos que se encuentran en el centro.
Notación: X
Ejemplo:
De una caja de números para un sorteo se sacaron de la urna los siguientes números:
· 4, 4, 7, 7, 8, 8, 12, 13, 13, 14, 15, 17, 17, 19, 23, 25, 25 = 13
· 5, 7, 8, 11, 11, 12, 13, 14, 16, 20 = 11+12= = 11.5
En el caso anterior como son dos datos se suman y se dividen entre dos.
MODA
Para datos no agrupados la moda es representada por el dato que más veces se repite en una serie de números, ejemplo:
Pilar tiene su boleta de calificaciones y son las siguientes:
10, 8, 9, 10, 10, 10, 9, 10, 10, 10
La moda es el numero 10, pues el que más se repite
Puede ser:
· Amodales: cuando no hay ningún número que se repita,
Ejemplo:
1,2,4,5,6,8,9,10,15,3,19,27,73,81,11 en este caso no se repite ningún numero
· Modales: cuando se repite un solo número.
Ejemplo:
1,2,4,5,6,8,9,17,3,54,69,57,52,5 solo se repite un numero y es el 5
· Bimodales: cuando se repiten dos números las mismas veces.
Ejemplo:
7,6,9,5,8,12,16,14,9,54,65,32 14 se repiten las mismas veces el mismo numero,9 y 14
· Multimodal: cuando se repiten más de dos números distintos las mismas veces.
Ejemplo:
8,5,95,85,64,25,36,98,78,48,54,25,95,62,63,64,85,3,99,1,1. Se repiten varios números las mismas veces

PARA DATOS AGRUPADOS
MEDIA
Para datos agrupados la formula es:
=
Ejemplo:
De los datos recolectados por los alumnos de la primaria de San Lucas de todos los grupos mostraron que de 0-10 estudiantes 5 obtuvieron baja calificación, de 10-20, obtuvieron un promedio alto y así sucesivamente hasta llegar a los 100 estudiantes con el siguiente promedio: 21 excelente, 27 bueno, 31 regular, 35 bajo, 21 muy malos, 14 fueron los peores, 9 en regularización y 5 no se presentaron. Ordene sus intervalos y obtenga la media de los datos agrupados
MEDIANA
Se obtiene mediante una distribución de frecuencias con la siguiente fórmula:
X= L + C
Donde:
X= mediana
L= límite real del intervalo que contiene a la mediana.
N= número de datos.
Fa= frecuencia acumulada que contiene a la mediana del intervalo anterior.
f = frecuencia del intervalo que contiene a la mediana.
C= tamaño del intervalo.
Ejemplo:
En una fabrica localizada en la comunidad de San Pedro, se venden canteras de diferentes medidas, se realizo un censo de acuerdo a sus pedidos y se obtuvo la siguiente tabla:
Identificamos los datos de la formula:
n= = 90.5
L= 150
fa= 64
C= 10
f =33
Sustituimos y resolvemos:
X= 150 + 10
X= 150 + 10
X= 150 + 0.803 (10)
X= 158.03
Moda
Se obtiene de la diferencia de donde ubicamos a la moda y de la frecuencia del intervalo anterior.
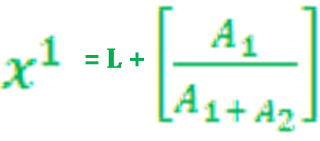
Donde:
= moda
= diferencia de donde ubicamos a la moda y la frecuencia del intervalo anterior.
= diferencia de donde ubicamos a la moda y la frecuencia del intervalo siguiente.
C= tamaño del intervalo.
L= limite real de clase.
Ejemplo:
En una tienda de ropa “la moda” se obtuvieron los siguientes datos:
Obtenemos a delta 1 y a delta 2, identificando al dato de mayor frecuencia restándolo al dato anterior a este y al dato siguiente del mismo.
=96-80 =96-55
= L + { }+c
=6000 + { }+1000
=6719.29
GRAFICAS
Las graficas tienen por objeto representar las características esenciales de los resultados obtenidos en la tabulación y dentro de ellos tenemos: grafica de barras, histogramas, polígonos de frecuencia, ojiva o circulo grama o grafica de pastel.
GRAFICA DE BARRAS
Se emplea para representar las frecuencias relativas y absolutas de acontecimientos y se utiliza en dos ejes, uno vertical y otro horizontal, en el eje X u horizontal se representan los intervalos, clases o tipos de resultados o acontecimientos y en la línea vertical las frecuencias de acuerdo al número de veces de cada resultado dejando un espacio entre cada barra, por ejemplo:
En él en un salón de belleza que está en alcuco asisten a la semana personas de diferentes edades como se presenta en el siguiente cuadro:
HISTOGRAMAS
En estadística, un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, normalmente señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos. Tiene por diferencia a la grafica de barras que estas van juntas ya que no permite huecos.
CIRCULOGRAMA
Las Gráficas circulares denominadas también gráficas de pastel o gráficas del 100%, se utilizan para mostrar porcentajes y proporciones.
Ejemplo:
Al realizar un estudio sobre el color de gelatinas que vende don chuy se obtuvieron los siguientes datos:
Son aquellos intervalos conformados por un extremo inicial y uno final, ejemplo:
Inicial 114-120 final
INTERVALO DE CLASE
Tienen correspondencia con los valores cuantitativos porque se agrupan de la misma manera y con el mismo tamaño.
RANGO
Para comenzar con la tabulación y poder obtener el tamaño del intervalo primero se obtiene el rango, el cual resulta con el dato mayor menos el dato menor de un conjunto, ejemplo:
Tenemos un conjunto de datos tales como:
50,23,35,41,11,25,41,43,86,22,17,56,20,26,25,90
90 – 11 = 80 + 1
DM Dm
Cabe mencionar que al rango se le tiene que sumar la unidad para determinar el tamaño del intervalo posterior.
Posteriormente debemos sacar el número de clase calculando la raíz cuadrada del total de datos:
Numero de clase: 16 = 4
Para obtener el intervalo se debe dividir el rango entre el número d clase:
Rango
Numero de clase
Tamaño del intervalo: =20.25 20
NOTA: cuando el intervalo cae en número par se debe subir al número non siguiente
intervalo
11-30
31-50
51-60
61-80
81-100
Como se puede observar, entre cada espacio de los intervalos existe una diferencia de 20, el cual es el valor obtenido anteriormente
Kendall y Buckland (citados por Gini V. Glas / Julian C. Stanley, 1980) definen la estadística como un valor resumido, calculado, como base en una muestra de observaciones que generalmente, aunque no por necesidad, se considera como una estimación de parámetro de determinada población; es decir, una función de valores de muestra.
• LA ESTADÍSTICA DESCRIPTIVA, que se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos en estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de parámetros estadísticos
son: la media y la desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide poblacional, clúster, etc.

• LA INFERENCIA ESTADÍSTICA, que se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas si/no (prueba de hipótesis), estimaciones de características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o moldeamiento de relaciones entre variables (análisis de regresión). Otras técnicas de moldeamiento incluyen anova, series de tiempo y minería de datos.
Población:
Una población se precisa como un conjunto finito o infinito de personas u objetos que presentan características comunes.
"Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales intentamos sacar conclusiones". Levin & Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común". Cadenas (1974).
Ejemplo:
Tomemos en cuenta a los alumnos de la EPO 165, la cual seria nuestra población.
"Se llama muestra a una parte de la población a estudiar qué sirve para representarla". Murria R. Spiegel (1991).
Muestreo:
Esto no es más que el procedimiento empleado para obtener una o más muestras de una población; el muestreo es una técnica que sirve para obtener una o más muestras de población.
Este se realiza una vez que se ha establecido un marco muestral representativo de la población, se procede a la selección de los elementos de la muestra aunque hay muchos diseños de la muestra.
Al tomar varias muestras de una población, las estadísticas que calculamos para cada muestra no necesariamente serían iguales, y lo más probable es que variaran de una muestra a otra.
Ejemplo;
Consideremos como una población a los estudiantes de la Preparatoria 165 determino por lo menos dos caracteres ser estudiados en dicha población;
· Religión de los estudiantes
· Sexo.
Variables y Atributos:
Las variables, también suelen ser llamados caracteres cuantitativos, son aquellos que pueden ser expresados mediante números. Son caracteres susceptibles de medición. Como por ejemplo, la estatura, el peso, el salario, la edad, etc.
Según, Murray R. Spiegel, (1992) "una variable es un símbolo, tal como X, Y, Hx, que puede tomar un valor cualquiera de un conjunto determinado de ellos, llamado dominio de la variable. Si la variable puede tomar solamente un valor, se llama constante."
Todos los elementos de la población poseen los mismos tipos de caracteres, pero como estos en general no suelen representarse con la misma intensidad, es obvio que las variables toman distintos valores. Por lo tanto estos distintos números o medidas que toman los caracteres son los "valores de la variable". Todos ellos juntos constituyen una variable.
Los atributos también llamados caracteres cualitativos, son aquellos que no son susceptibles de medición, es decir que no se pueden expresar mediante un número.
IUTIN (1997). "Reciben el nombre de variables cualitativas o atributos, aquellas características que pueden presentarse en individuos que constituyen un conjunto.
Las variables y su medición:
Una variable es un símbolo, tal como X, Y, H, x ó B, que pueden tomar un conjunto prefijado de valores, llamado dominio de esa variable. Para Murray R. Spiegel (1991) "una variable que puede tomar cualquier valor entre dos valores dados se dice que es una variable continua en caso contrario diremos que la variable es discreta"
Las variables, también llamadas caracteres cuantitativos, son aquellas cuyas variaciones son susceptibles de ser medidas cuantitativamente, es decir, que pueden expresar numéricamente la magnitud de dichas variaciones. Por intuición y por experiencia sabemos que pueden distinguirse dos tipos de variables; las continuas y las discretas
Las variables continuas
se caracterizan por el hecho de que para todo para de valores siempre se puede encontrar en valor intermedio, (el peso, la estatura, el tiempo empleado para realizar un trabajo, etc.)
Ejemplo:
En la Primaria "Francisco I. madero" de la comunidad de San Joaquin se levanto el siguiente censo a los niños que asisten hay
Niño Peso Talla
José 18, 300 1,15
Julio 20,500 1,20
Pedro 19,000 1,10
Las variables discretas
serán aquellas que pueden tomar solo un número limitado de valores separados y no continuos; son aquellas que solo toman un determinado números de valores, porque entre dos valores consecutivos no pueden tomar ningún otro; por ejemplo el número de estudiantes de una clase es una variable discreta ya que solo tomará los valores 1, 2, 3, 4... Nótese que no encontramos valor como 1,5 estudiantes.
Datos Estadísticos:
Los datos estadísticos no son otra cosa que el producto de las observaciones efectuadas en las personas y objetos en los cuales se produce el fenómeno que queremos estudiar. Dicho en otras palabras, son los antecedentes (en cifras) necesarios para llegar al conocimiento de un hecho o para reducir las consecuencias de este.
Los datos estadísticos se pueden encontrar de forma no ordenada, por lo que es muy difícil en general, obtener conclusiones de los datos presentados de esta manera. Para poder obtener una precisa y rápida información con propósitos de descripción o análisis, estos deben organizarse de una manera sistemática; es decir, se requiere que los datos sean clasificados. Esta clasificación u organización puede muy bien hacerse antes de la recopilación de los datos.
Ejemplo:
Se quiere sacar un censo a las personas de San Lucas y los datos a preguntar serian: su edad, estado civil,etc... Vemos pues que la clasificación marca la pauta de la clase de datos que debe ser obtenido.
CLASIFICACIÓN DE LOS DATOS
Los datos estadísticos pueden ser clasificados en cualitativos, cuantitativos, cronológicos y geográficos.
Datos Cualitativos
cuando los datos son cuantitativos, la diferencia entre ellos es de clase y no de cantidad.
Ejemplo:
Si deseamos clasificar los estudiantes que cursan la materia de estadística con la profesora Pilar por su estado civil, observamos que pueden existir solteros, casados, divorciados, viudos.
Datos cuantitativos
Cuando los valores de los datos representan diferentes magnitudes, decimos que son datos cuantitativos.
Ejemplo:
Se clasifican los estudiantes del Núcleo San Juan de acuerdo a sus notas, observamos que los valores (nota) representan diferentes magnitudes.
Datos cronológicos
cuando los valores de los datos varían en diferentes instantes o períodos de tiempo, los datos son reconocidos como cronológicos.
Ejemplo:
Al registrar los promedios de notas de los Alumnos de la escuela de San Lucas de en los diferentes semestres.
Datos geográficos
Cuando los datos están referidos a una localidad geográfica se dicen que son datos geográficos.
El número de estudiantes de educación superior en las distintas regiones del país.
Ejemplo
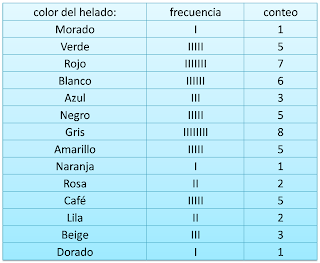
Juan tiene una peletería y le preguntaron de qué color de helados es el que más se vende, y esto fueron los resultados obtenidos:
SE OBTUVO LA SIGUIENTE FRECUENCIA
Juan tiene una paletería y le preguntaron de qué color de helados es el que más se vende, y esto fueron los resultados obtenidos:
se obtuvo la siguiente table de frecuencias: